复分析 部分题型整理
哈哈我学不完啦
Ch1 复数与复变函数
1.1 复数的定义及其运算
证明复数不等式
合理利用三角不等式(命题1.1.4,p3)
1.2 复数的几何表示
求几何图形对应的复数方程
- 习题1.2.14


用复数证明几何定理
(感觉不是很重要,就不上图了)
- 例1.2.1
- 例1.2.2
1.3 扩充平面和复数的球面表示

用球面表示求距离/证明性质
貌似都是爆算……
Ch2 全纯函数
2.1 复变函数的导数
2.2 C-R 方程
研究函数可微性
法1:用定义
- 习题2.1.1
法2:用实可微 + C-R方程(\(\Leftrightarrow \frac{\partial f}{\partial \overline{z}}=0\))
- 例2.2.5
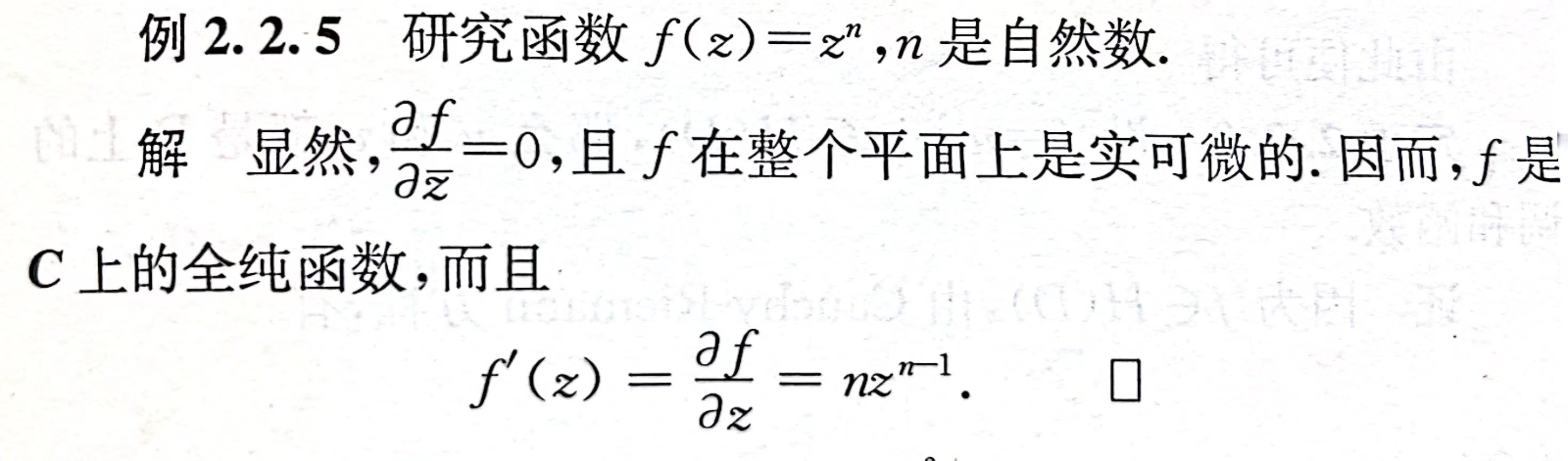
- 例2.2.6
研究函数\(f(z)=e^{-|z|^2}\)

证明是/不是调和函数
法1:用定义
法2:用 \(u\in C^2(D),\Delta u=4\frac{\partial ^2 u}{\partial z \partial \overline z}\)
2.4 初等全纯函数
单值解析分支存在性
定理:
(PPT 4,5 - P6)
定理:如果D是不包含原点和无穷远点的单连通域,那么Logz在D上有单值全纯分支。(PPT 4,5 - P9,书本 P54)
根号多值函数的单值解析分支问题
定理:
单值解析分支求值
法1:已知一个值,利用简单路径辐角求其他值
法2:直接计算
共形映射区域变换
- 例2.4.5

- 例2.4.6

2.5 分式线性变换
区域变换
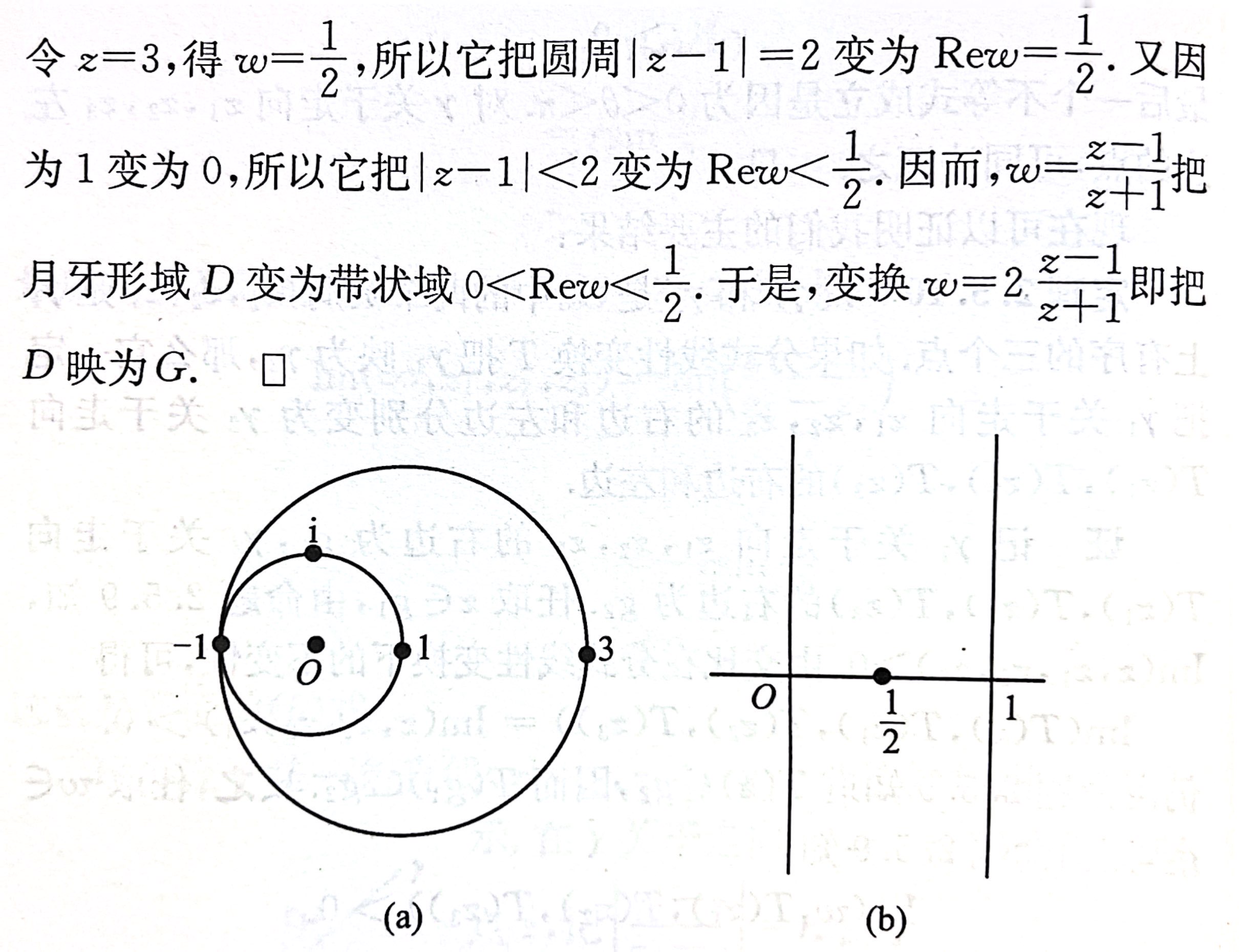
法1:利用边界
- 例2.5.11

- 习题2.5.3

充分性:利用该映射把实轴映为实轴,找 \(z_1,z_2,z_3\rightarrow w_1,w_2,w_3\) 直接算出分式线性变换,再利用唯一性。
法2:利用对称点
- 例2.5.15

- 例2.5.16

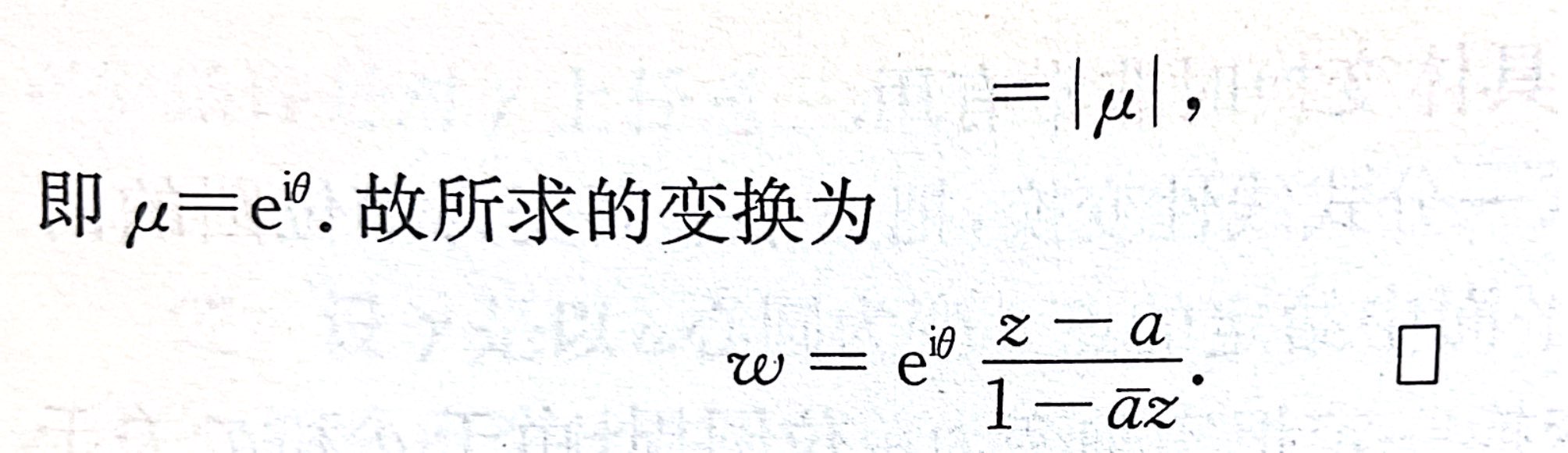
- 例2.5.17
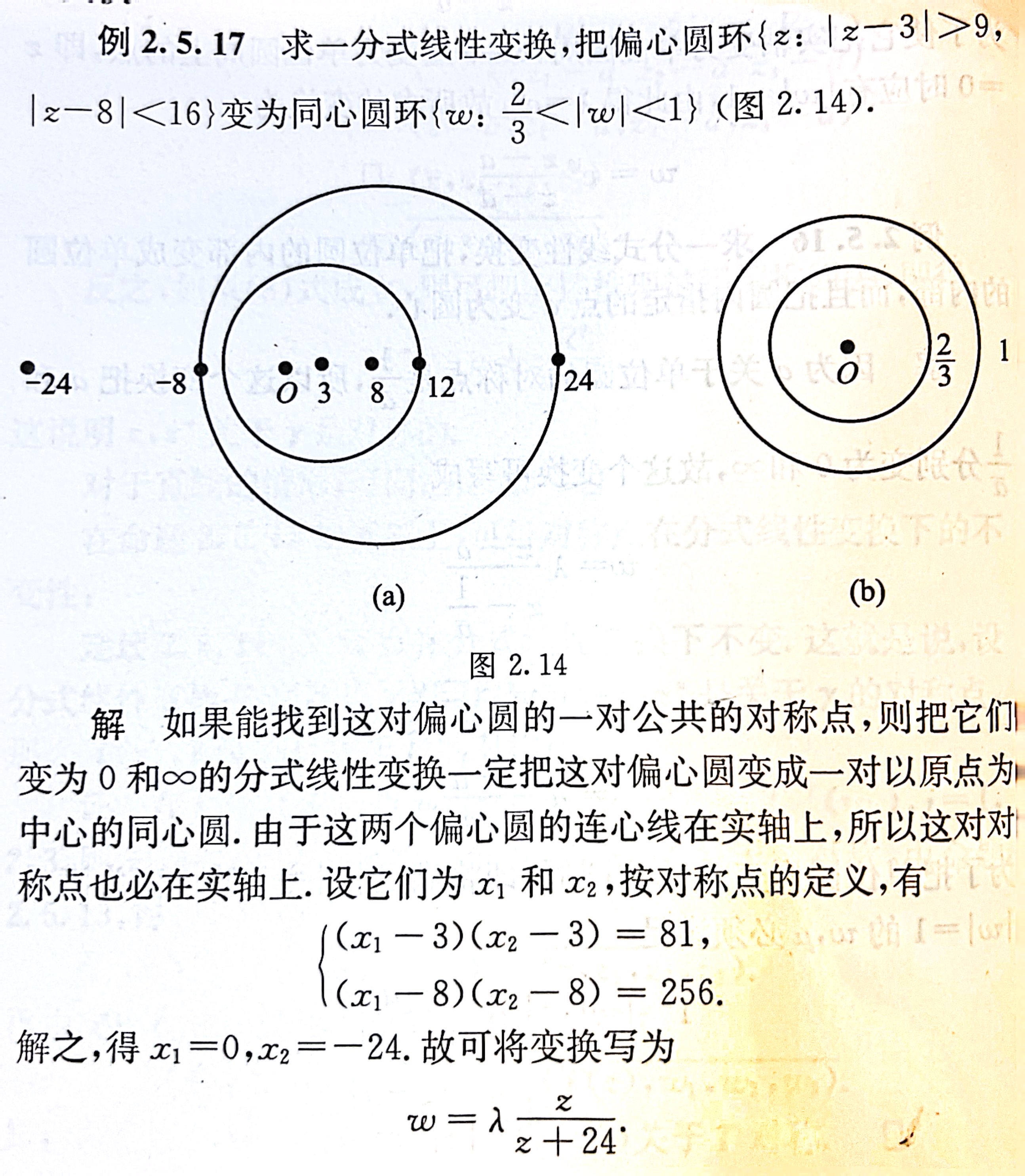

法3:找对应点,待定系数
- 习题2.5.20

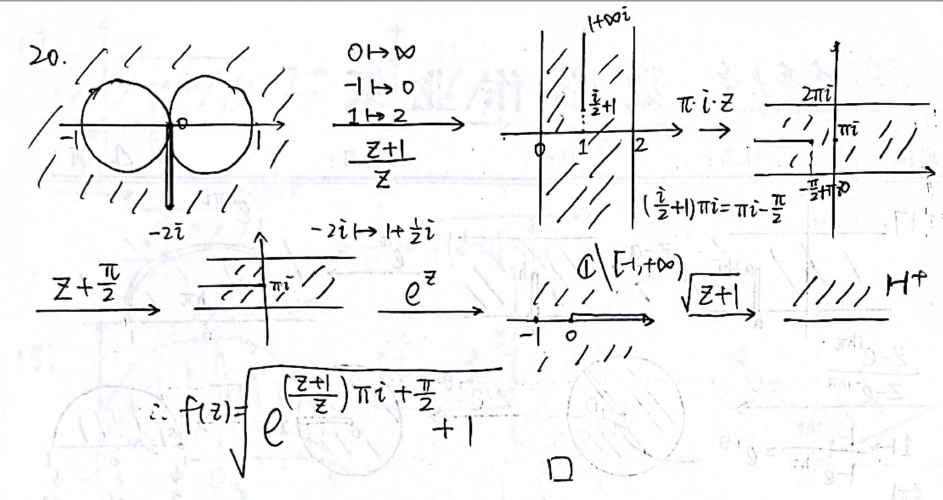
法4:结合共形映射和分式线性变换(不知道怎么归类捏)
- 习题2.5.17


- 习题2.5.18

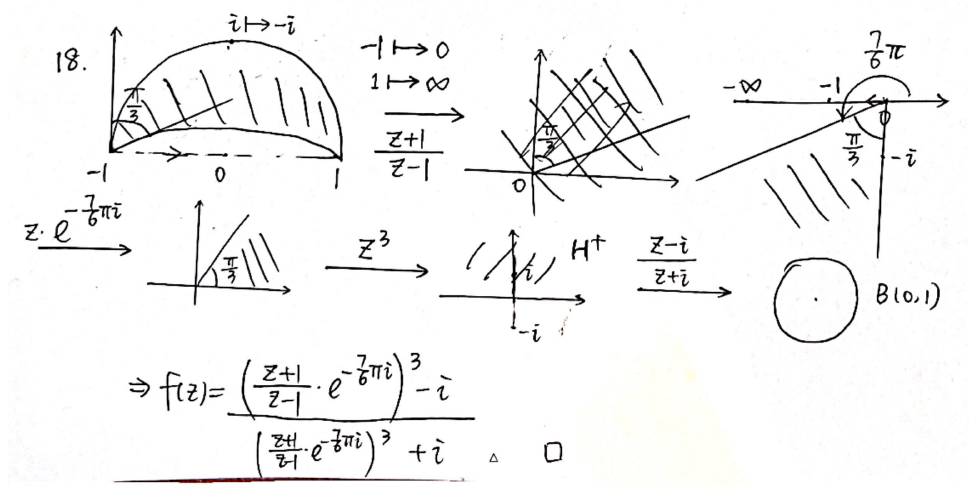
Ch4 全纯函数的 Taylor 展开及其应用
4.4 辐角原理和 Rouche 定理
求零点个数
利用 Rouche 定理
注意选取函数 \(f(x),g(x)\),记得做必要的放缩。
- 例4.4.12
- 例4.4.13
利用辐角原理
先取简单闭曲线,证明简单闭曲线上没有零点,再计算围绕简单闭曲线走一圈的辐角变化,用辐角原理解零点个数。
- 例4.4.14